2.3 Шкала интервалов

Во многих случаях нет возможности измерить сами величины наблюдаемых размеров, но возможно (если есть необходимость) измерять только отличия (разницы) между познаваемыми сопоставлением размерами. При этом используется так называемая шкала интервалов.

На измерительной шкале интервалов фиксируются отличия сопоставляемых размеров. Эта форма отображения величин измеряемого является более совершенной, так как на шкале интервалов есть условные, но вполне определенные единицы измерений, что позволяет количественно (численно) охарактеризовать соотношение исследуемых размеров.

Математическая запись сравнения между собой двух однородных размеров по их разнице имеет вид

∆Qi,j = Qi -Qj

По шкале интервалов определяют такие соотношения размеров, как: равно (=), не равно (≠), больше (>), меньше (<), сумма (+),разница (-).

Следовательно, здесь определено отношение порядка и эквивалентности не только между размерами характеристик качества, но и между расстояниями между ними на шкале измерений.

Упорядоченные ряды, например, пяти разных размеров по их 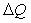 могут быть такими:

∆Q1,2 < ∆Q2,5  < ∆Q3,5 < ∆Q4,3 ,

или ∆Q4,3 > ∆Q3,5 > ∆Q2,5  > ∆Q1,2.

Графическое построение шкалы интервалов рассматриваемых размеров показано на рис. 2.1.

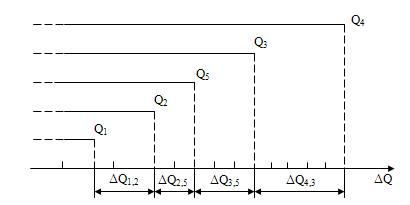
Рис.2.1. Схема построения шкалы интервалов

 При таком построении шкалы интервалов, когда нет начала отсчета и нет соответствующей физической единицы измерений (меры), за единицу измерений принимается некоторая произвольно выбранная величина. Несмотря на значительную неопределенность измеряемых разностей размеров в условных единицах, результаты измерений по шкале интервалов более информативны по сравнению с измерениями по шкале порядка, так как они позволяют не только установить, что один размер больше или меньше другого, но и численно определить, на сколько единиц (мер) отличаются исследуемые размеры один от другого.

С данными, полученными по шкале интервалов, можно производить не только логические, но и арифметические действия, например, складывать и вычитать величины. Однако по шкале интервалов нельзя определить, во сколько раз данный размер больше или меньше другого, так как неизвестными остаются величины сопоставляемых размеров.

Часто при решении измерительной задачи требуется более жесткая "привязка" результатов, получаемых по шкале интервалов, к определенному (произвольно выбранному или предпочтительному) размеру. Этот выбранный размер является опорным (базовым), по сравнению с которым определяют отличия других размеров. Отметка базового размера на измерительной шкале (линейной, круговой или цифровой) представляет собой реперную точку. Эта реперная точка, если она одна на шкале интервалов, обычно принимается за начало отсчетов.

На рис. 2.2 иллюстрировано построение шкалы интервалов с началом отсчета от размера Q5.

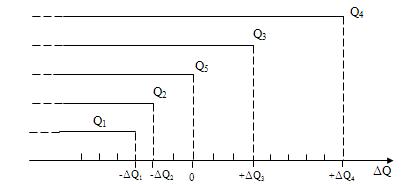
Рис. 2.2 Построение шкалы интервалов с нулевой отметкой

 Если принять на базовый размер Q2, то начало отсчета сместится влево, а если Q3, то вправо. Следовательно, начало отсчета на шкале интервалов устанавливается произвольно. При этом так же произвольно выбирается единица измерений интервалов - их величины на шкале измерений принимают наименьший интервал сопоставляемых размеров.

Примерами шкал интервалов с одной реперной точкой являются календари летоисчислений. В христианском календаре за нулевую точку отсчета принят год рождения Христа ("от рождества Христова").

Зачастую. с целью приближения единицы измерений по шкале интервалов к реальности, за меру измеряемых интервалов берут долю и некоторую часть чего-либо (предпочтительного) интервала размеров. Для этого на шкале измерений устанавливаю две реперные точки Qp1 и Qp2, расстояние между которыми выражает разницу двух выбранных размеров. Промежуток между реперными точками градируется, т.е. делится на равные или (реже) пропорциональные части.

Градация есть установление масштаба на шкале интервалов. Масштаб, то есть одна часть выбранного интервала между двумя базовыми (опорными) размерами, принимают за меру - за единицу измерений.

Схема создания такой двухреперной шкалы интервалов приведена на рис. 2.3.

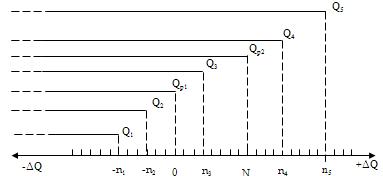
Рис.2.3. Шкала интервалов с двумя реперными точками

 Классическим примером измерений по шкале интервалов с двумя реперными точками является измерение температур по шкале Цельсия. Здесь в качестве опорных размеров взяты температуры замерзания (таяния льда) и кипения чистой воды. Интервал между этими температурами разделены на 100 равных частей. Одна часть, принятая за единицу измерения температур, была названа градусом. Шкала Цельсия неограниченно распространяется за пределы температур 0%100°С при условии, что любые значения температур измеряются единицами, равными 1/100 части интервала температур от замерзания до кипения воды.

В интервальной шкале Рюмера для измерения температуры в качестве реперной точки с нулевым значением показателя также принята температура таяния льда, а за интервал масштаба - температуры от таяния льда до температуры кипения воды. Однако этот интервал масштаба разделен не на 100 частей, как в системе Цельсия, а на 80 градаций (градусов).

Шкала интервалов может иметь и несколько реперных точек, но в этом случае возникает проблема согласования единиц измерения размеров в пределах различных интервалов такой многореперной шкалы.

Ввиду неопределенности или условности начала отсчета математические операции умножения и деления результатов измерений, полученных с помощью шкал интервалов, осуществить нельзя. Следовательно, по шкале интервалов нет возможности определить, во сколько раз один размер больше или меньше другого.

2.4 Шкала отношений

Для того чтобы определить не только на сколько, но и во сколько раз один размер больше или меньше другого, или количественно измерить величину размера в официально выбранных единицах измерения, необходимо воспользоваться шкалой отношений.

Шкала отношений - это измерительная шкала, на которой отсчитывается (определяется) численное значение величины qi как математического отношения измеряемого размера Qi  к другому известному размеру, принимаемому за единицу измерения [Q].

В метрологии и квалиметрии считается, что «любое измерение по шкале отношений предполагает сравнение неизвестного размера с известным и выражение первого через второй в кратном или дольном отношении».

Математическая запись измерения по шкале отношений имеет вид:

,

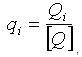где  i = 1, 2, 3,   n - это номер измеряемого размера.

Шкала отношений - это шкала интервалов, в котором определен нулевой элемент - начало отсчета, а также размер (масштаб) единицы измерений [Q].

По шкале отношений определяются такие значения измеряемых размеров, как: равно (=), не равно (≠), больше (>), меньше (<), сумма (+), разница размеров (-), умножение (*), деление (:). Следовательно, с относительными величины измеряемых размеров можно проводить многие логические и все арифметические действия.

Предельный интервал величин q измеряемых размеров по шкале отношений - от нуля до (возможно) бесконечности, поэтому, в отличие от шкалы интервалов, на шкале отношений нет отрицательных значений. Число qi, определено по шкале отношений, соответствует величине измеренного размера Qi, выраженного в единичных размерах [Q]. Следовательно, измерения по шкале отношений имеют вид, показанный на рис. 2.4.

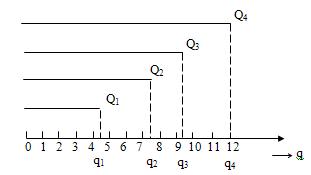
Рис. 2.4. Схема измерений по шкале отношений

 Так как со qi значениями возможны логические и все арифметические операции: сложение, вычитание, умножение, деление, поэтому шкала отношений является наиболее совершенной и широко применяемой. Однако построение шкалы отношений и измерение с ее помощью не всегда возможны. Например, время измеряется только по шкале интервалов, а вес обычно измеряется по шкале отношений, хотя его можно измерить и по шкале интервалов, так как шкала отношений является частным случаем шкалы интервалов.

Измерение интервала по шкале отношений осуществляют по формуле (теоретической модели) вида:

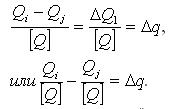
Следует отметить, что численное значение q измеряемой величины может быть различным в зависимости от принятого размера единицы измерения [Q]. Так, например, 1 метр длины может быть выражен еще и в таких величинах, как 100 см, 1000 мм или 0,001 км.

Итак, шкала отношений универсальна, так как по ней можно сформировать ранжированные ряды (шкалы порядка) возрастающих или сокращающихся размеров, вычислить интервалы отличий (как и по шкале интервалов) тех размеров, которые измерены по шкале отношений и, наконец, определить численные значения измеренных размеров в относительных величинах.

Шкала отношений наиболее приемлема для измерений большинства показателей качества, особенно для таких численных характеристик, как геометрические размеры объектов, их плотность, сила, напряжение, частота колебаний и прочие.