Во многих случаях
напрямую измеряется величина чего-либо. Например, непосредственно
подсчитывается число дефектов в изделии, количество единиц произведенной
продукции, сколько студентов присутствует на лекции, количество прожитых лет и
т.д. и т.п. При таких измерениях на измерительной шкале отмечаются абсолютные количественные
значения измеряемого. Такая шкала абсолютных значений обладает и теми же
свойствами, что и шкала отношений, с той лишь разницей, что величины,
обозначенные на этой шкале, имеют абсолютные, а не относительные значения.
Результаты измерений
по шкале абсолютных величин имеют наибольшую достоверность, информативность и
чувствительность к неточностям измерений.
Шкалы интервалов,
отношений и абсолютных величин называют метрическими, так как при их построении
используются некоторые меры, т.е. размеры, принятые в качестве единиц
измерений.
Измерительные шкалы,
основанные на использование рядов предпочтительных чисел, обычно являются
метрическими шкалами интервалов или абсолютных величин, исчисляемых, например,
единицами допусков измеряемых линейных размеров или квалитетами.
Предпочтительными называют
числа, наиболее часто используемые в технике, в технологии, в науке и других
сферах деятельности людей. Предпочтительные числа представляют собой
определенное множество взаимосвязанных чисел (ряд чисел), которые обладают
систематизированным свойством, что позволяет использовать их при выборе, назначении
и измерении размеров различных величин. Такие математические ряды чисел
формально характеризуют различные зависимости и закономерности изменений в
реальном мире. Чаще всего математические выражения измеряющихся состояний имеют
вид простой арифметической (линейной) или геометрической (нелинейной)
прогрессии.
Ряды чисел
арифметической прогрессии имеют постоянную разницу между двумя соседними
числами. Ряд чисел геометрической прогрессии отличаются тем, что произведение
или частное любых двух чисел ряда всегда является членом этого ряда. Например:
и т.д. Любой член (число) геометрической прогрессии, возведенной в целую
положительную или отрицательную степень, также является членом этой прогрессии:
и т.д. Итак, геометрическая прогрессия - это ряд последовательно возрастающих
или убывающих чисел с постоянным отношением между двумя соседними числами. Это
отношение является знаменателем прогрессии и обозначается буквой. Следовательно,
каждый член геометрической прогрессии является произведением предыдущего члена
на .
В связи с
перечисленными свойствами геометрической прогрессии зависимости, определяемые
из произведений членов или их целых степеней, всегда подчиняются закономерности
этого ряда. Например, если ряд будет определять линейные размеры, то площади
или объемы, образованные из этих линейных величин, также подчиняются его
закономерности.
Так как везде принята
десятичная система счета чисел, начиная с единицы, то наиболее удобными
являются геометрические прогрессии, включающие число 1 и имеющие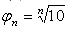 
с n , кратным 10. Международная
организация по стандартизации (ISO или по-русски ИСО) установила (рекомендация
Р ИСО 497) четыре основных десятичных ряда предпочтительных чисел с такими
знаменателями :
В отдельных
обоснованных случаях допускается использование рядов R80 с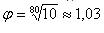 
и R160 c 
.
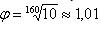Следует отметить, что
установленные ИСО ряды предпочтительных чисел основаны не только на десятичной
системе счета, но и на принципе оптимальных соотношений, который реализован,
например, в "золотом сочетании". Под "золотым сочетанием"
понимают прямоугольник со сторонами a и b, которые соотносятся между собой как:
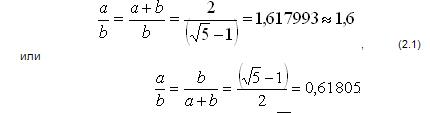
Равенству (2.1)
соответствует выражение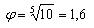 
. Исходя из этого еще в XIX веке французский инженер-механик
Шарль Ренар предлагал унифицировать диаметры (толщины) тросов для аэростатов и
парусного флота по закону геометрической прогрессии, в которой знаменатель был бы равен соотношению "золотого
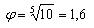сечения", где с . Только много лет спустя, в середине ХХ века, с целью
обеспечения единства в применении геометрической прогрессии для нормирования
геометрических параметров технических изделий и их контроля точности Ш.Ренара
было принято и реализовано через требования национальных (государственных) и
международных стандартов на продукцию.
Итак, наиболее
применяемые ряды предпочтительных чисел, их знаменатели и количество чисел в
рядах с интервалом от 1 до 10 приведены в табл.2.1.
Предпочтительные
знаменатели геометрических прогрессий
Любой член ряда Ni
геометрической прогрессии находится по формуле:
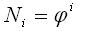
Ряды предпочтительных
чисел используются для установления унифицированных размеров сверл, фрез,
разверток, зенкеров и других инструментов, а также размеров и допусков
(отклонений) деталей машин, изделий в целом, технических параметров (свойств)
продукции, процента дефектности в партиях продукции, величин напряжений
электрического тока, номинальных значений длин электромагнитных волн
радиовещательных диапазонов и т.д.
Не случайно поэтому
числа номинальных значений радиовещательных диапазонов и грузоподъемности
железнодорожных цистерн Р имеют сходные величины, такие как:
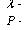
80 т, 63 т, 50 т, 40
т, 32 т, 25 т, 20 т, 16 т, 12 т, 10 т.
Следует отметить, что
на практике используются не только ряды типа R. Так, например, в радиотехнике
часто применяют предпочтительные числа рядов Е, установленных Международной
электротехнической комиссией (МЭК):
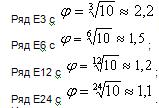
Иногда используют так
называемые ступенчатые и прерывистые ряды предпочтительных чисел. Ступенчатый
ряд - это когда параметрический ряд характеристик продукции задают вначале
одним рядом предпочтительных чисел (например, R5), а по достижению определенного
значения параметра, переходят к другому ряду (например, R10). Прерывистым рядом
предпочтительных чисел является тот, в котором опускается некоторое количество
членов ряда.
Измерение какого-либо
параметра, заданного предпочтительным числом, можно осуществить по шкале с
градацией по существующим предпочтительным числам. Такую шкалу квалиметрических
измерений называют шкалой предпочтительных чисел.
Известно, что
номинальные линейные размеры (диаметры, длины, глубины, расстояние между осями
и т.д.) изделий, их частей, отдельных деталей и соединений в соответствии с
требованиями стандартов назначаются равными предпочтительным числам того или иного
ряда R. Эти номинальные размеры являются базовыми, по отношению к которым
назначаются допуски разрешенных наклонений. Фактически отклонения должны быть в
пределах допусков, и этим оценивается точность изготовленных изделий.
Номинальным размером
называется размер, которым служит началом отсчета отклонений и относительно
которого определяются предельные размеры.
Отклонением размера
называется алгебраическая разность между действительным (наибольшим или
наименьшим) и соответствующим номинальным размером.
Допустимая разность
между верхним (наибольшим) и нижним (наименьшим) предельными значениями
размеров называется допуском. Допуск - это величина, в пределах которой может
колебаться размер детали или другого изделия, сохраняя заданные эксплуатационные
характеристики.
Градация допусков
осуществлена в виде набора классов, или степеней точности. Под степенью
точности понимают совокупность допусков, соответствующих одному относительному уровню
точности для определенного качества номинальных размеров. Степень точности
геометрического размера характеризуется величиной допуска (выраженного в
микрометрах) для заданного номинального размера.
Степень точности
геометрических размеров (характеризуемая величиной допуска, выраженного в
микрометрах) для установленного количества номинальных размеров называется квалитетом
и обозначается буквами IT - сокращение от слов ISO Tolerance (ИСО допуск).
Под квалитетом
понимают совокупность допусков, характеризуемых постоянной относительной
точностью для всех номинальных размеров установленного диапазона. Иначе говоря,
квалитет - характеристика точности изготовления изделий (например, детали), определяющая
соответствующие методы и средства обработки, а также контроля качества
обработки. Единой системой допуска и посадок (ЕСДП), основанной на системе
допусков ИСО, для размеров от 1 до
Таким образом,
степень точности лилейных размеров изделий можно оценивать как по допустимым и
действительным отклонениям от номинальных размеров, то есть как по шкале
абсолютных значений допусков, так и по линейной шкале абсолютных значений
квалитетов. При этом номинальный размер и номер квалитета выступают в качестве
метрической меры точности или степени точности, с помощью которой определяется
уровень соответствия измерительного размера требуемому размеру.
Градация
измерительной шкалы допусков имеет вид геометрической прогрессии, а шкала квалитетов
равномерная (шкала арифметической прогрессии).
